为什么C++直接输出2¹⁰⁰⁰可以精确到个位

这个想法源于一道程序设计课的上机题：任意给定一个正整数N(N<=100)，计算2的n次方的值。 这道题的本意是练习高精度计算，但是可以发现，使用long double类型调用pow函数就足够了。当然我还是用高精度计算写的。 然而，我发现即使仅使用double，甚至用float，在C++中都可以输出正确的答案。 运行下面的C++代码：

#include<iostream>
#include<cmath>

using namespace std;

int main(){
    int x;
    cin>>x;
    cout.precision(0);
    cout<<fixed<<pow(2,x);
    return 0;
}

输入1000，程序输出一个超过300位的结果，虽然这早已超出double和long double的精度，但是运算结果是完全正确的。

至于结果的正确性，比较方便的方法就是与Python给出的结果进行对比。在Python的控制台中输入2**1000可以直接得到高精度计算的结果，很方便。

为什么结果是精确的呢？

我尝试用同样的方法计算3的n次方，发现只有前几位是正确的，而且最后一位数是偶数。

这样原因就很显然了：和计算机中浮点数的表示方法有关。

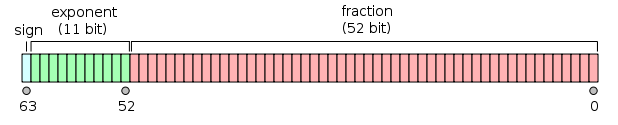
我们知道数字在计算机中是以二进制的形式存储的。浮点数大致是以\((-1)^\text{sign}\times\text{fraction}\times 2^\text{exponent}\)的形式表示的，如图：（图片引用自维基百科）

用浮点数表示2的n次方的时候，尾数部分取1即可，即\(1\times 2^n\)，所以不会损失精度。

打一个比方，在十进制中，我们把34500000000写成科学计数法，保留三位小数，即3.45e10，不会损失精度；但是如果我们把34512345678写成科学计数法，保留三位小数，也是3.45e10，这样就会损失精度了。正如34500000000在十进制中是一个很“整”的数，2的n次方在二进制中也是很“整”的数。

顺便说一下，二进制中只有表示成分数后分母是2的n次方的小数才能够写成有限位小数，例如\(0.5625=\frac{9}{16}=(0.1001)_2\)。然而在十进制中像0.1、0.2这样的有限位小数转换成二进制数都是无限循环小数，例如\(0.1=(0.0001100110011…)_2\)，从而这样的数在浮点数中不能完全精确的表示。

当用cout输出时，因为已经指定了precision(0)和fixed，程序在打印浮点数的时候会以精确到个位的十进制数打印出来，自然也就是精确的了。高精度计算是在“二进制转换为十进制”的过程中发生的。

我试着把程序改成调用long double类型的pow函数，这样最多可以计算到2的16383次方，结果也是完全精确的。