我在百度贴吧Mathematica吧的这个帖子看到有人在研究如下问题:
求解所有系数为1或-1的n次多项式的根,然后把所有这样的根绘制到复平面上。
我想起以前在Matrix67的博客上也看到过这个问题,里面介绍了Sam Derbyshire用Mathematica跑了四天四夜(也有说法是三天三夜)生成了n=24的所有根,然后用Java程序绘图,得到了下图:
贴吧中的“三分钟复现”是算到n=17的情况。由于n增加1导致需要求解方程的数量翻倍,每个方程中根的个数也增加1,所以我估计了一下,n=24时大约需要求出24*2^24=402M个解。(24次多项式包括常数项有25个系数,但是由于对称性可以省去一半计算。)这些计算显然不需要以天为数量级的时间。
我决定用C语言解决这个问题,同时改善一下显示的效果,并尝试绘制分辨率更高的图。
解决这个问题有两个比较麻烦的事:
- 如何求解多项式的根
- 图上的颜色按照什么绘制
第一个问题我查找了一些方案,最后觉得boj的建议比较好:使用GNU Scientific Library库。这个库里面有很多科学计算的函数,其中的gsl_poly_complex_solve就可以求解多项式的根。
于是我写出求解多项式的程序,这个程序把所有的根都以二进制形式直接保存在文件中。fork出8个进程可以把CPU跑满。
注:请在cygwin或linux下编译,编译出错请先检查是否正确安装GSL库,然后尝试在编译命令中加 -lgsl -lgslcblas -lm 参数
/*程序功能:求解所有指定次数的、系数为-1、1的多项式,并把复数解保存到r[0-7].data中
输出格式:二进制文件,顺序排列每个解(double)的实部和虚部*/
#include <stdio.h>
#include <gsl/gsl_poly.h> //GNU science library 多项式
#include <sys/wait.h>
#include <unistd.h>
#define deg 24 //多项式次数
int main(){
int i,j,p,total;
double a[deg+1],z[deg*2]; //a:多项式系数 z:求解结果
FILE *fp;
char fn[10];
a[deg]=1.0; //减少一半运算
for(p=0;p<8;p++){
if(fork()==0){
sprintf(fn,"r%d.data",p);
fp=fopen(fn,"wb");
for(i=0;i<3;i++) //该进程的三个确定系数
a[deg-1-i]=(p&(1<<i))?1.0:-1.0;
total=(1<<(deg-3));
for(i=0;i<total;i++){
for(j=0;j<deg-3;j++)
a[j]=(i&(1<<j))?1.0:-1.0;
gsl_poly_complex_workspace *w=gsl_poly_complex_workspace_alloc(deg+1);
gsl_poly_complex_solve(a,deg+1,w,z); //求解
gsl_poly_complex_workspace_free(w);
fwrite(z,sizeof(double),deg*2,fp);
if(i%10000==0)printf("Process%d : %.2f%%\n",p,i*100.0/total);
}
printf("Process%d : Completed\n",p);
exit(0);
}
}
while(wait(NULL)>0); //等待其他进程
return 0;
}
程序几分钟就跑完了,生成了6G的数据。
然后想办法解决第二个问题。
首先要弄明白图中的颜色表示什么。一个像素的颜色表示那个像素范围内根的密度。所以简单的办法就是按照期望的分辨率(例如2000*2000)建立一个二维数组,然后根据每个根的位置统计每个像素范围内根的个数。
那么又如何根据根的个数算出颜色?颜色值是有范围限制的,例如0~255,所以我想到计算根个数的最大值。但是经过测试发现,画出的图很暗,几乎看不清,只有某些点处是亮的,这说明根聚集在某些点处,这些点附近根的个数和其他平凡点附近根的个数之比可能是发散的,不能通过统计最大值来决定颜色。
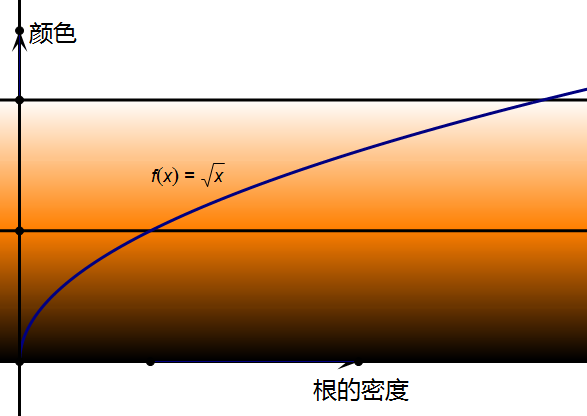
我直接手工设定了一个亮度的微调值,调节到比较满意的位置。根的个数从少到多,颜色从黑色渐变到橙色(RGB=255,127,0),超过设定值的少量部分再渐变到白色。测试发现暗部不清楚,于是用平方根函数把亮度往上调了一下(和开根号再乘以10的调分方法一个道理)。
根的密度和颜色的关系如下图所示:
程序如下:
/*程序功能:根据r[0-7].data中的复数数据,生成密度图*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define DIM 1024 //图片分辨率 DIM*DIM
#define RANGE 2.0 //绘制范围 x,y∈[-RANGE,RANGE]
#define B 12.0 //亮度微调参数,越大越暗
#define BUFFSIZE ((1<<24)*24/8*2) //读文件缓冲区大小,24次多项式约800M
double *data; //读文件缓冲区
int (*den)[DIM]; //像素点范围内根的个数
unsigned char (*bitmap)[DIM][3]; //用于生成位图
int total=0,max;
void countroot(int cnt){ //按照像素区域对方程的根计数
double x,y;
int i,px,py;
for(i=0;i<cnt;i++){
x=data[i*2];
y=data[i*2+1];
px=DIM/2*x/RANGE+DIM/2; //计算对应的像素坐标
py=DIM/2*y/RANGE+DIM/2;
if(px>0&&px<DIM&&py>0&&py<DIM)
den[px][py]++;
}
total+=cnt; //总点数计数
}
void colorfunc(int d,unsigned char *color){ //根密度与颜色的映射函数
int t;
t=(long long)255*sqrt((double)d/max);
if(t<256){ //黑至橙渐变
color[0]=t;
color[1]=t/2;
color[2]=0;
}else if(t<512){ //橙至白
color[0]=255;
color[1]=128+(t-256)/2;
color[2]=t-256;
}else{ //白
color[0]=color[1]=color[2]=255;
}
}
void genpic(){ //根据密度数据生成位图
int i,j;
printf("Generating pic...\n");
max=B*total/DIM/DIM; //颜色255对应的根密度
for(j=0;j<DIM;j++)
for(i=0;i<DIM;i++)
colorfunc(den[i][j],bitmap[j][i]);
}
void savefile(){ //保存文件
char fn[20];
sprintf(fn,"roots_%d.ppm",DIM);
FILE *fp=fopen(fn,"wb");
printf("Saving to %s...\n",fn);
fprintf(fp,"P6\n%d %d\n255\n",DIM,DIM);
fwrite(bitmap,1,DIM*DIM*3,fp);
fclose(fp);
printf("Completed!\n");
}
int main(){
int p,cnt;
char fn[10];
FILE *fp;
data=malloc(BUFFSIZE*sizeof(double));
den=malloc(DIM*DIM*sizeof(int));
bitmap=malloc(DIM*DIM*3);
if(!data||!den||!bitmap){
printf("Out of memory!\n");
exit(-1);
}
for(p=0;p<8;p++){
sprintf(fn,"r%d.data",p);
printf("Loading : %s\n",fn);
fp=fopen(fn,"rb");
fseek(fp,0,SEEK_END); //定位到文件尾
cnt=ftell(fp)/sizeof(double)/2; //根据文件大小计算数据量
fseek(fp,0,SEEK_SET); //定位到文件头
fread(data,sizeof(double),2*cnt,fp);
fclose(fp);
printf("Loaded, count=%d\n",cnt);
printf("Processing : %s\n",fn);
countroot(cnt);
}
genpic();
savefile();
return 0;
}
运行结果:
注:分辨率太高之后有些图片查看器可能不识别,我测试命令行版的ffmpeg可以打开,商业软件Photoshop更方便一些。
如果不考虑磁盘读写(中间文件我保存在了ramdisk),生成几万乘几万分辨率的图也不过几分钟。
后来我又跑了n=26的情况,发现除了细节放大后比较平滑之外没有显著区别,故不单独贴图。但是运行到98%时遇到了一个错误:
gsl: zsolve.c:78: ERROR: root solving qr method failed to converge
Default GSL error handler invoked.
并不是内存不足或溢出导致,应该是GSL解某个方程时出了问题。
有人问我为什么不是计算出根分布后直接统计并生成图片,而是保存中间文件。我觉得程序在运行时经常需要用同一组数据生成不同分辨率的图片,所以前者反而不方便。
最后贴几张细节图,感受一下数学之美:

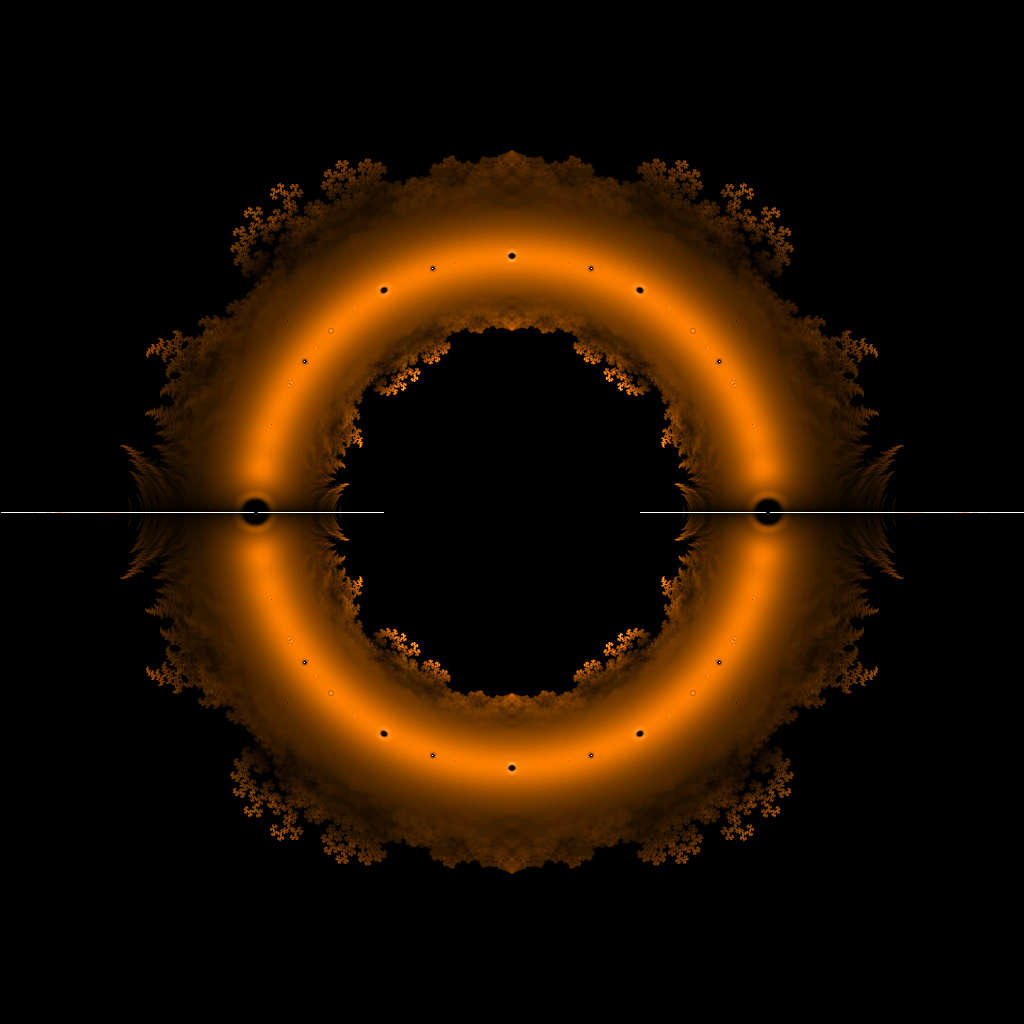
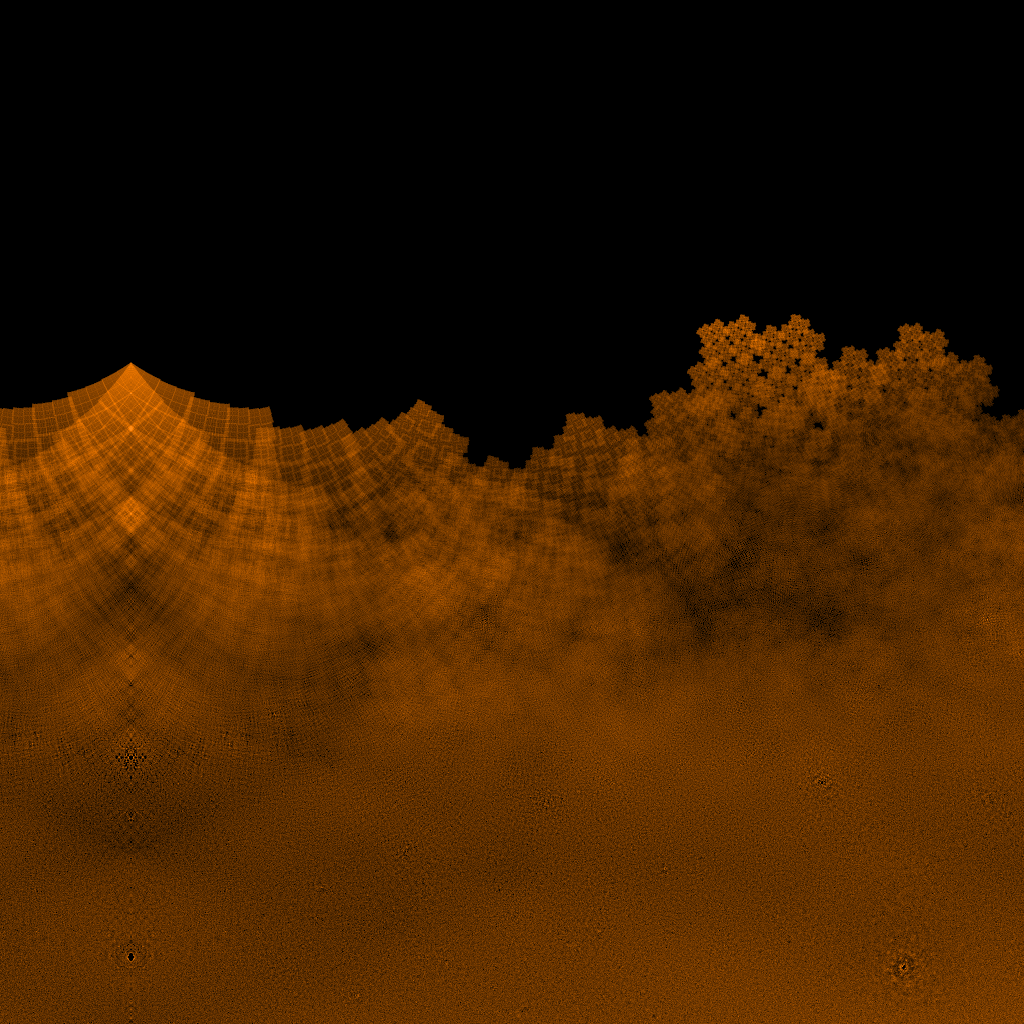
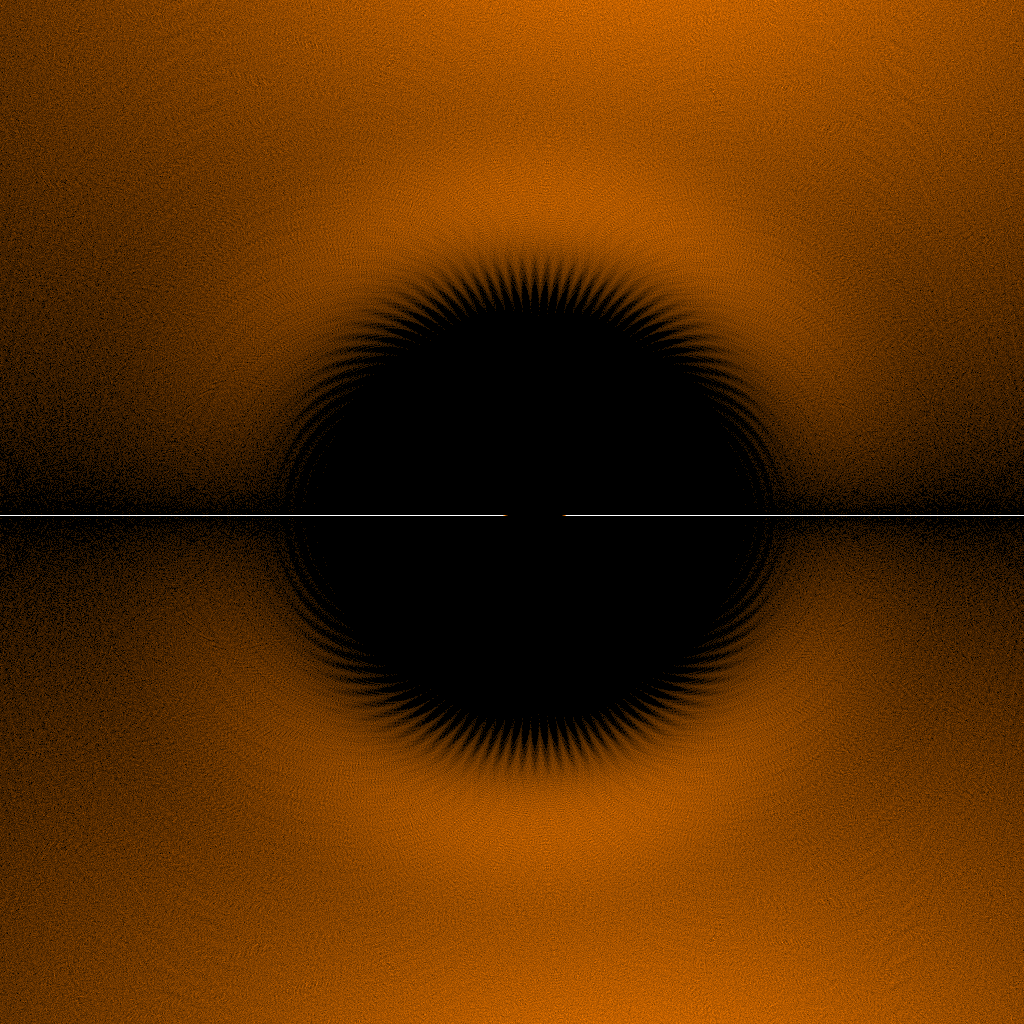

Getting patterns in a structured problem is ordinary.. It should not be described as “the Beauty of Math”….