昨天数学分析课上讲了“距离”概念的推广。
广义的“距离”(明可夫斯基距离)定义为
$${P_\alpha }\left( {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)} \right) = {\left( {{{\left| {{x_1} – {x_2}} \right|}^\alpha } + {{\left| {{y_1} – {y_2}} \right|}^\alpha }} \right)^{\frac{1}{\alpha }}}$$
其中\(\alpha =1\)时为曼哈顿距离,\(\alpha =2\)时为欧氏距离。
对于不同的“距离”可以画出对应的单位圆(即到原点“距离”为1的点的集合)
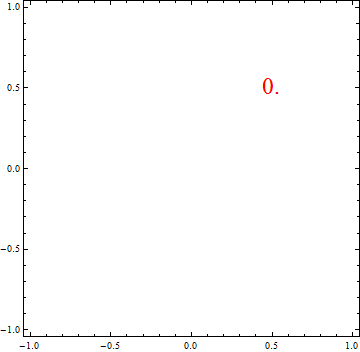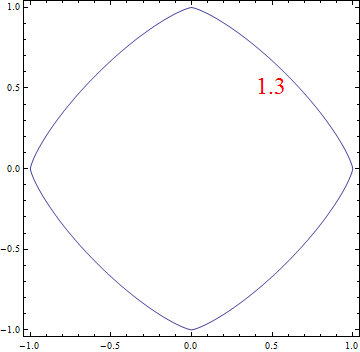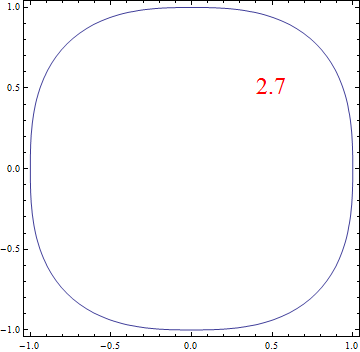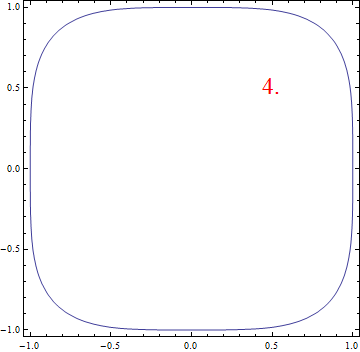
当\(\alpha\)从0变化到4时,单位圆的形状的变化很有趣,我做了下面的动态图:
注:\(\)\alpha <1[/latex]时不满足“距离”的定义,但是也可以画出对应的单位圆。
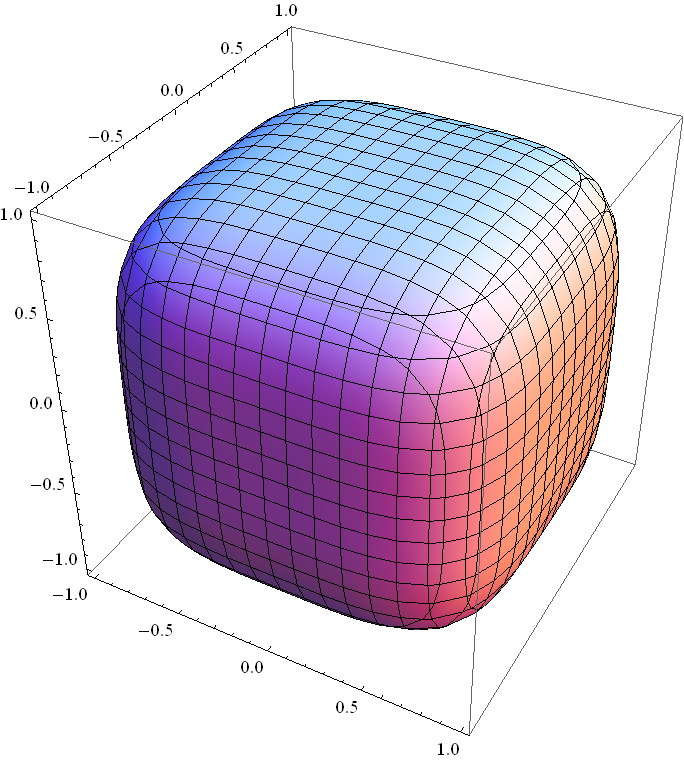
如果把这种“单位圆”推广到三维空间,也可以作出很有趣的图,例如下面是[latex]x^4+y^4+z^4=1[/latex]的图像:
圆角矩形